MATEMATICAMENTE

5.Bko Paulak Matemáticamente liburua ekarri zuen eskolara. Asko gustatu zitzaigun eta poliki poliki lantzen ari gara.

AMAGOIAK tangram erakutsi zigun eta oso zaila izan zen zeren piezita asko zeuden. Eta asko konplikatu ginen. Beste joku geometriko batzuk ere egin genituen. Oso zailak!

Etxean ere Tangramekin irudiak osatu genituen.

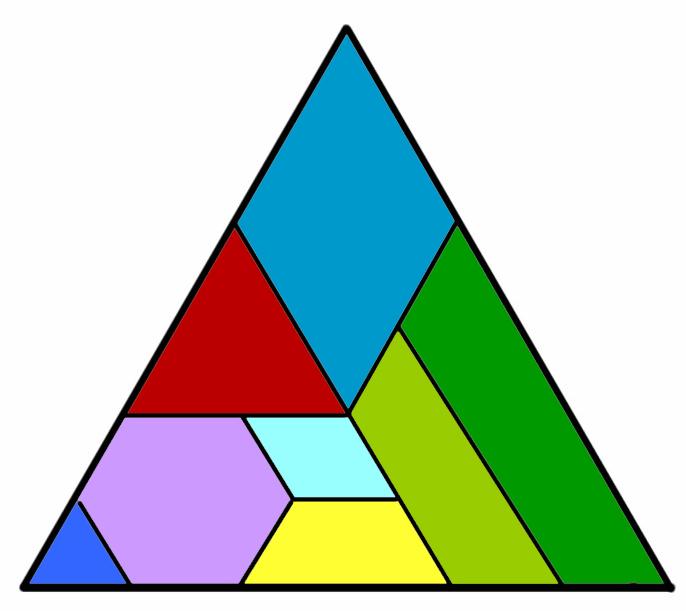Hementxe daukazue beste TANGRAM mota  bat

 IANIREK Sujiko eta Karuro erakutsi zizkigun zenbakizko joku batzuk ziren:

Ez zen batere erreza!

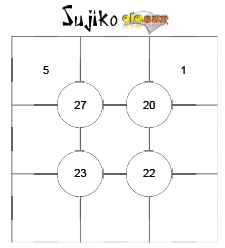
Instrucciones Sujiko: Coloca los números del 1 al 9 en las casilla vacías, sin repetir ninguno, para que los círculos interiores sumen las cantidades indicadas

Ea lortzen duzuen!







LUCÌAK erakutsi zizkigun hiruki ekilateroa edo aldeberdina, hiruki eskalenoa, hiruki isoszelesa eta hiruki zuzena.

Zenbat hiruki daude multi-hiruki honetan?

LEIREK zeroa nola sortu zen adierazi zigun.

ZEROAREN SORRERA

• Lehen zantzuak Mesopotamian (K.a. 700) eta Grezian (K.o. 150) kokatzen dira.
• Maien zenbaki-sisteman erabiltzen zen zeroa adierazteko sinbolo bat.
• Nolanahi ere, VII. mendean Indian hedatu zen zeroaren erabilera.

Zeroarekin guk erabiltzen dugun ZENBAKUNTZA SISTEMA lortu zen, bestela ezinezkoa da.
Gure sistema da zeroa duen bakarra. Babilonian, egipziarrek, erromatarrek, mayaterrek... ez zuten zeroa erabiltzen. Horregatik eragiketak beste era baten egin behar ziren.
Eta ... esaten dugu ZEROA EZ DUELA EZERTARAKO BALIO!


EKAIK infinitoari buruz hitz egin zigun arratsalde batean.

Joaquín Sabinak abesti batean esaten duen bezala: "SIN CERO Y SIN INFINITO", edo hobeto esanda "DESDE EL CERO AL INFINITO"
Del latín infinitus, infinito es aquello que no tiene (ni puede tener) término o fin. El concepto se utiliza en diversos ámbitos, como la matemática, la filosofía y la astronomía.
Los números ordinales son aquellos que indican la posición de un elemento en una sucesión ordenada que se extiende hasta el infinito. En general puede decirse que los números siempre son infinitos, ya que su sucesión no encuentra límite. En otras palabras: si uno comienza a contar (1, 2, 3…), deberá decidir cuándo detenerse ya que, de lo contrario, siempre existirá un número que le siga al último. 

Olatzek "NEURRIEI BURUZ" hitzegin zigun: altuera, luzera, denbora...
Orain arte ez dugu esan, baina horrelako aurkezpenak egiten ditugunean, apunteak hartzen ditugu. Ondoko argazkietan Olatz ikusiko duzue baita beste guztiok apunteak hartzen ere.

Zenbaki segidak

Iratik erakutsi zigun, zenbakien gauza interesgarriak eta bitxiak. Progresio aritmetika eta geometrika zer den.

Internet-en hauen definizioak bilatu ditugu: 

.Zenbaki errealen segida orori progresio esaten zaio. Progresioen taldean bi bereizi behar ditugu, bere propietateen definizioa sistematizatzen duen erregulartasun printzipioa adierazten dutelako: progresio aritmetikoak eta progresio geometrikoak. Segida aritmetikoa poliko doa hazten, geometrikoa berriz oso azkar.

1-2-3-4-5... progresio aritmetikoa da (+ 1)

2-4-8-16-32-64--- progresio geometrikoa da (x 2)

Iratik ere zera esan zigun: Malthusek 1798.urtean munduko elikagaiak progresio aritmetikoan handitzen direla eta biztanlegoa berriz progresio geometrikoan esan zuen, horrek pobrezia eta gosea ekarriko zituela esan nahi zuen,

J

Pablo eta bere radembo ,(DENBORA, ordenagailu honek noiz behinka ez digu kasurik egiten eta hizkiak aldatzen ditu, je, je):

Egipziarren egutegia, Lurraren errotazio mugimendua eta orduak, zenbat minutu eta segundu dituen ordu batek... gauza guzti hauek azaldu zizkigu Pablok.

Munduko bolarekin denborarekin lotutako beste kontzeptu batzuk ere gogoratu genituen: eguna, gaua, urtaroak, ekinoccioa (irailaren 21ean eta martxoaren 21ean, gutxi gora behera) eta solstizioa (abenduaren 21ean eta ekainaren 21ean, berriz gutxi gora behera).
Neguko solstizioan (abenduan) egunik motzena eta gaurik luzeena.
Udako solstizioan (ekainean) egunik luzeena eta gaurik motzena.
Udaberriko eta udazkeneko ekinozioetan gauak eta egunak iraupen berdina dute.

ALBAK Pascalen hirukia adierazi zigun.

Blaise Pascal frantses matematikaria zen. Hiruki honen kasila bakoitza lortzeko goiko bi kasilen zenbakien batura egin behar dugu. 

Lehen 16 errenkadak osatu ondoren, hiruki honek oso ezaugarri bereziak dituela baieztatu genuen. Ea zuek aurkitzen dituzuen!

ANEK PI zenbakia zer den kontatu zigun. Horretarako zirkunferentzia eta zirkuluaren arteko desberdintasunak azaldu zituen. Pi zenbakia kalkulatzeko ezinbestekoa zen jakitea zer diren diametroa, erradioa eta zirkunferentziaren perimetroa.

Ondoren zirkunferentzia desberdinak egin genituen. Perimetroa zati diametroa egin eta zenbaki guzti hauek atera zitzaizkigun,

Ia, ia PI zenbakia (sokarekin ez genuen oso zehazki egin).

PI-k infinito hamartar ditu, baina guk esaten dugu 3,1416 dela.

Makil batekin eta gometsak jarriz lurrean zirkunferentziak egin genituen.

ERIKen eskutik papiroflexia egin genuen: zelorik gabeko beste kubo mota bat, edo hobeto esanda Hexaedro. Erik oso trebea da!
 Egun horretan 6.Bko ikasleak ere gurekin egon ziren. Ikasle asko izan zituen Erik-ek, baina guztiak oso erne egon ziren.

Beste egun batean arrautzen "esperimentua" egin zigun. 
Zenbat liburu eutsiko ziren arrautzen gainean?
Begiratu argazkietan, guk ezin genuen sinetsi!

HARITZEK zenbakien segidei buruz hitz egin zigun eta ariketa batzuk jarri zizkigun:

HARITZEKIN Fibonacci ezagutu genuen. 

Leonardo Pisano (Pisa, Italia, 1170 - 1250), Leonardo Bonacci, Leonardo Fibonacci edo Fibonacci moduan ezaguna, Italiar matematikaria izan zen, Erdi Aroko ezagunetarikoa. Ezaguna da batez ere bi aurkikuntzengatik:

• Hindu-arabiar zenbaki sistema Europan sartu zuen eta berau erabiltzeko bideak jarri zituen XIII. mendeko Liber Abaci liburuaren bitartez.
• Fibonacciren zenbakiak deskribatu zituen liburu berean, nahiz eta berak ez zituen aurkitu baizik eta adibide moduan jarrii

Hauxe da Fibonacciren segida: 1, 1, 2, 3, 5, 8, 13...

Zeinztzuk dira hurrengo zenbakiak?

Fibonacci ere oso ospetsua zen bere espiralarengatik eta PHI zenbakiarengatik.

IZASKUNekin berriz geometriari ekin genion.

Labirintoei buruz hitz egin zuen, ariketa zail bat jarri zigun eta ondoren KRETAKO labirintoa nola egiten den erakutsi zigun. NAHIAk bitartean KRETAKO MINOTAUROaren istoria kontatu zigun.

Eta... Geometriarekin jarraituz JONEk oso gai interesgarria ekarri zigun: EZINEZKO IRUDIAK, gazterelaz esanda FORMAS IMPOSIBLES. Buruhauste galanta eduki genuen¡

Zer iruditzen zaizkizue hauek?




NAHIAK zenbaki lehenak ekarri zizkigun. Hau adierazi zigun:

Zenbaki lehenak, batez (1) eta bere buruaz bakarrik zatigarriak diren zenbakiak dira, eta zenbaki arrunten multzoaren azpimultzo bat osatzen dute. Eratostenes-en bahea egin genuen 0tik 100arteko zenbaki lehenak ateratzeko.
Zenbaki lehenak, batez (1) eta bere buruaz bakarrik zatigarriak diren zenbakiak dira, eta zenbaki arrunten multzoaren azpimultzo bat osatzen dute. Aurreneko hogei zenbaki lehenak honakoak dira: 2,3,5,7, 11, 13, 17, 19, 23, 29, 31, 37, 41 , 43, 47, 53, 59, 61, 67 eta 71. Bata ez da lehena, zatitzaile bakarra duelako, eta zeroa ere ez, zeroz zatigarri den zenbakirik ez dagoelako.

Saio horretan ere 6.Bko ikasleak gurekin egon ziren. Begiratu zein irakasle ona den Nahia, guztiak jo ta ke lanean!

SOUADekin SUDOKUak egin genituen.
Sudokua buruhauste matematikoa da eta, bere helburua, 3x3ko karratu txikiz osatutako 9x9 tamainako koadrikula osatzea da. Karratu txiki horietan, 1 eta 9 arteko zenbakiak ipini behar dira, beti ere ilara edota zutabe berberean zenbaki berdina errepikatu gabe.
Maila desberdinetako Sudokuak daude: hastapena, erreza, erdikoa, zaila eta "experto".
Gelako kide batzuk zailak egin zituzten.

Denborarik baduzue... hemen dituzue sudoku batzuk:


IKER eta ANEk 3D zer den azaldu zuten. Jarduera konplexu bat proposatu ziguten eta hori egiteko Mate-gelan ditugun MULTI-LINK kubitoak atera genituen.
Eskerrak Iker honetan oso trebea dela eta laguntza handia eskaini zigula.

DIEGOK beste lan mota bat egin zuen:
Aurreko ikasturtean INTXAURRONDOKO ZINEMALDIA antolatu genuen eta pelikulak ikusteko sarrerak salduz diru pixka bat lortu genuen (sarrerak oso merkeak zien: 0,10zentimo).
Diegok txanponak sailkatu eta oso ondo antolatu ondoren, dirua zenbatu zuen eta diru horrekin KLARION MAJIKOAK erostea pentsatu zuen.

Klarion majikoak jolastokian erabiltzeko BAIMENA zuzendariari eskatu zion idatziz.

Zuzendariak erantzun zion.

KLARIONAK erabiltzeko argibideak ingelesez idatzirik zeudenez Iñigori laguntza eskatu genion.

DIEGOK Haur Hezkuntzako 4 eta 5 urtetako haurrekin jolasteko ZIRKUITU bat diseinatu zuen.

Zirkuitoa jolasgaraian margotu eta... JOLASTERA!

ZIRKUITOA ondo ikusteko BETAURREKO MAJIKOAK ere behar genituen.

 Zein ondo pasa genuen!!!